|
|
Tepelná konvekce
K nerovnovážným dějům dochází při zahřívání kapaliny a následném konvekčním proudění uvnitř kapaliny. V závislosti na uspořádání experimentu dochází k následným typům nestabilit, při nichž můžeme pozorovat vznik charakteristických struktur.
1. Rayleighova - Bénardova nestabilita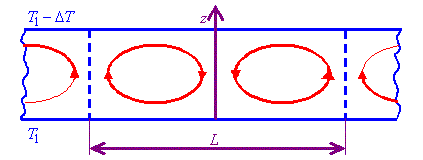 obr. 1 obr. 1
Kapalina vyplňuje nádobu tvořenou dvěma horizontálními deskami
dobře tepelně vodivými a bočními stěnami s nízkou tepelnou vodivostí.
Dno nádoby je zahříváno. Teplota kapaliny u dolní destičky je T1 u horní destičky T2, přičemž T1 > T2.
Systém charakterizuje tzv. Rayleighovo číslo (Ra):
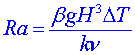 , ,
kde 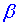 je součinitel teplotní roztažnosti, g je konstanta tíhového zrychlení, H výška vrstvy kapaliny, k součinitel teplotní vodivosti, je součinitel teplotní roztažnosti, g je konstanta tíhového zrychlení, H výška vrstvy kapaliny, k součinitel teplotní vodivosti,
v součinitel kinematické viskozity a 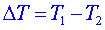 . .
Při Ra = 0 se systém nachází v rovnovážném stavu.
Při 0 < Ra < Rakr (malá hodnota rozdílu T ) se otevřený systém
nachází v nerovnovážném stavu. Povrch kapaliny zůstává v klidu. Závislost
teploty na vzdálenosti ode dna nádoby je dána vztahem: 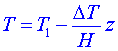 , kde z je souřadnice vertikální osy, T1 je teplota kapaliny u dna nádoby (T1 se zahříváním dna
zvyšuje) a teplo se šíří vedením (kondukcí) v souladu s Fourierovým zákonem vedení tepla. , kde z je souřadnice vertikální osy, T1 je teplota kapaliny u dna nádoby (T1 se zahříváním dna
zvyšuje) a teplo se šíří vedením (kondukcí) v souladu s Fourierovým zákonem vedení tepla.
Při Ra = Rakr (dosáhne-li Ra kritické hodnoty) tíha horní vrstvy kapaliny převládne nad dosud stabilizujícími
viskózními silami. V systému nastává proudění (konvekce).
Ohřev spodních vrstev kapaliny vede ke
snížení hustoty a jejich stoupání působením vztlaku směrem
vzhůru. Chladnější vrstvy v horních částech kapaliny klesají směrem ke dnu. Proti tomuto pohybu částí kapaliny
působí viskózní síly a chaotický pohyb molekul. Výsledkem těchto opačných tendencí je
makroskopický pohyb kapaliny ve tvaru válců. Za vhodných počátečních podmínek může Rayleighovo číslo dále stoupat a s
ním stoupá i počet konvekčních válců.
Kvantitativní popis Rayleighovy-Bénardovy nestability
Kvantitativně lze Rayleighovu-Bénardovu konvekci popsat pomocí systému nelineárních rovnic, vyjadřujících v podstatě bilancí hmotnosti, hybnosti a energie (s uvážením hraničních podmínek). Jsou to základní rovnice hydrodynamiky, tj. Navierova-Stokesova rovnice, rovnice kontinuity a rovnice vedení tepla.
Předpokladáme, že hydrodynamiku nehomogenní tekutiny, zejména charakter konvektivního toku v ní, lze v řadě případů popsat, jestliže tekutina splňuje Boussinesqovu aproximaci. Tehdy kromě její hustoty uvažujeme další látkové vlastnosti tekutiny konstantní a teplo vznikající jako důsledek vnitřního tření tekutiny zanedbáváme.
Navierova - Stokesova rovnice: 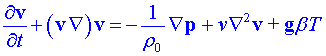 [s nelineárním členem [s nelineárním členem 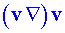 ] ]
Rovnice kontinuity: 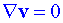
Rovnice vedení tepla: 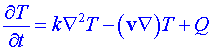 [s nelineárním členem [s nelineárním členem 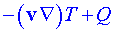 ]. ].
Zde je v lokální rychlost toku, v kinematická viskozita, ρo objemová střední hustota tekutiny, p tlak a T je termodynamická teplota .Sčítanec 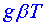 je výslednicí vztlakové a gravitační síly působící na jednotku hmotnosti; g je tíhové zrychlení, k tepelná vodivost, je výslednicí vztlakové a gravitační síly působící na jednotku hmotnosti; g je tíhové zrychlení, k tepelná vodivost,
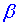 tepelná roztažnost a Q je tepelná funkce. Stupeň nehomogenity tekutiny charakterizuje výraz pro lokální hustotu tepelná roztažnost a Q je tepelná funkce. Stupeň nehomogenity tekutiny charakterizuje výraz pro lokální hustotu 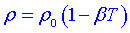 . .
Řešení těchto rovnic v analytickém tvaru je obtížné, proto se užívají numerické metody, nebo se výchozí rovnice zjednodušují. Příkladem zjednodušení je Lorenzův model.
Lorenzův model*
Po několika úpravách, substitucích a aplikaci Galerkinovy metody Lorenz nakonec získal soustavu tří obyčejných diferenciálních rovnic:
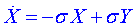 , ,
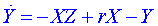 , ,
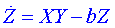 , ,
kde tečkou nad příslušnými koeficienty jsou vyznačeny derivace podle bezrozměrného času
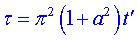 , pro r platí , pro r platí 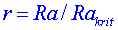 , , 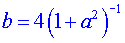 , , 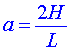 . .
Proměnná X odpovídá složce rychlosti toku (je úměrná úhlové rychlosti rotace konvektivní buňky v tekutině) a proměnné Y, Z odpovídají členům Fourierova rozvoje teploty: Y udává rozdíl teplot mezi výstupnými a sestupnými proudy v zahřívané tekutině a Z odchylku vertikálního profilu rozložení teploty od profilu lineárního.
Pokud zobrazíme závislost jednotlivých proměnných v trojrozměrném grafu, nevede křivka do jediného bodu, jak je tomu, ustálí-li se systém v rovnovážném stavu. Nevznikne ani limitní cyklus typický pro periodického chování. Namísto toho trojrozměrný graf zobrazuje složitou křivku s fraktálovou strukturou. Tvar křivky signalizuje naprostou neuspořádanost, neboť ani jeden bod obrazce se neopakuje (pak by se systém choval periodicky). Zároveň ovšem signalizuje nový druh uspořádanosti.
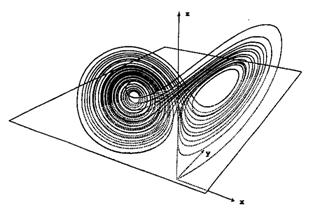 Na obrázku vlevo je fázový portrét Lorenzova atraktoru, získaný numerickou integrací systému rovnic pro parametry: Na obrázku vlevo je fázový portrét Lorenzova atraktoru, získaný numerickou integrací systému rovnic pro parametry: 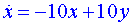 , , 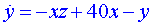 , , 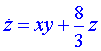 . .
Trajektorie řešení vycházející z počátečního bodu 0 = (0, 0, 0) v čase t = 0 nejprve udělá jednu smyčku doprava, potom několik oběhů vlevo. Poté opět vpravo a tak pokračuje dále zcela nepravidelně.
Na obrázku je 50 takových smyček; řešení, která leží pod rovinou z = 27, jsou vyobrazena tečkovaně. Jestliže místo počátečního bodu 0 = (0, 0, 0) vybereme jiný počáteční bod, blízký původnímu, nové řešení se od původního bude vzdalovat velmi rychle. Setkáváme se zde s citlivou závislostí na počátečních podmínkách.
obr. 2
* V rozsáhlé světové literatuře o chaotickém chování dynamických systémů je stále nejčastěji citovanou prací průkopnická práce E. N. Lorenze. Jejím původním cílem bylo na vhodném modelu ilustrovat potíže vznikající při numerické předpovědi počasí. Až později, poté co matematikové odhalili nesmírný význam myšlenek obsažených v práci, se prokázalo, že Lorenzova studie daleko překračuje rámec meteorologie a pronikavě zasahuje do dřívějších představ o topologii řešení nelineárních diferenciálních rovnic. Ještě do začátku šedesátých se předpokládalo, že topologie je vyčerpána singulárními trajektoriemi (uzlem, sedlem, ohniskem a limitním cyklem) a nesingulárními trajektoriemi, které se k singulárním trajektoriím přibližují nebo se od nich vzdalují. Právě Lorenzova práce, kde soustava rovnic vede na podivný Lorenzův atraktor, ukázala dosavadní omyl.
Lorenzovo vodní kolo
První slavný chaotický systém, objevený Edwardem Lorenzem, přesně odpovídá mechanickému zařízení: vodnímu kolu. Toto jednoduché zařízení je schopno překvapivě komplikovaného chování. Rotace vodního kola má některé vlastnosti společné s rotujícími válci tekutiny v procesu konvekce. Vodní kolo představuje vlastně řez tímto válcem. Oba systémy jsou poháněny rovnoměrně - vodou nebo teplem a oba uvolňují energii. Kapalina ztrácí teplo; nádoby ztrácejí vodu.
Dlouhodobé chování obou systémů záleží na tom, jak velká je hnací síla. Voda rovnoměrně stéká shora. Pokud je proudění vody do vodního kola pomalé, horní nádoba se dostatečně nenaplní, nepřekoná tření a kolo se neroztočí. (Stejně tak v tekutině, není-li teplo dostatečné, tekutina nepřekoná viskozitu a nedojde k pohybu).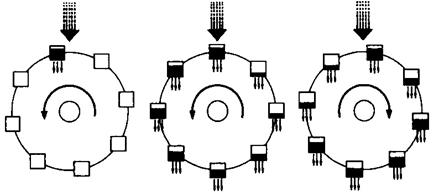
Je-li proudění rychlejší, hmotnost horní nádoby uvede kolo do pohybu (vlevo). Otáčky vodního kola mohou dosáhnout takové hodnoty, že pokračují rovnoměrnou rychlostí (uprostřed).
Je-li proudění ještě rychlejší, otáčení se v důsledku nelineárních účinků, zabudovaných do systému, může stát chaotickým. To, jak se nádoby naplní, když procházejí pod proudem vody, záleží na rychlosti otáčení. Jestliže se kolo otáčí rychle, nádoby mají málo času, aby se naplnily. (Podobně má tekutina v rychle se točícím konvekčním válci málo času na to, aby absorbovala teplo). Jestliže se kolo otáčí rychle, nádoby mohou začít stoupat na druhou stranu dříve, než se stačí vyprázdnit. Výsledkem je, že nádoby na druhé straně mohou otáčení zpomalit a poté obrátit jeho směr. Lorenz zjistil, že z dlouhodobého hlediska se smysl otáčení může změnit mnohokrát, otáčení se nikdy neustálí v rovnoměrném tempu a nikdy se neopakuje předpověditelným způsobem.
obr. 3
Význam Rayleighovy-Bénardovy nestability
Výzkum jevů, v nichž hraje roli Rayleighova-Bénardova nestabilita, má velký význam v meteorologii, oceánografii, při zabezpečování ventilace prostorů, ale také např. při vyšetřování růstu krystalů. V atmosféře ve vrstvě oblačnosti, která je v oblasti horního povrchu ochlazována dlouhovlnným vyzařováním, probíhají jevy, které lze rovněž uvažovat jako Bénardovu konvekci.
2. Bénardova-Marangoniova nestabilita
Ohřev dna nádoby, ve které se nachází tenká vrstva kapaliny s volným povrchem, může být příčinou dalšího typu uspořádání - vzniku struktury ve tvaru obrazce složeného z šestihranných buněk (také pětihranných i čtverců). Tyto buňky popsal jako první H. Bénard r.1900 a jsou dnes podle něho nazývané Bénardovými buňkami. Vznik Bénardových buněk lze dobře pozorovat ve viskóznější kapalině (oleji) s přimíchaným hliníkovým práškem. Ideální nádoba by měla mít homogenně tepelně vodivé dno, pokud možno tepelně nevodivé stěny, stačí však Petriho miska. Na následujícím obrázku vidíme vznik buněk, vlevo větší vertikální gradient teploty ( menší buňky), vpravo menší (větší buňky).
obr. 4   obr. 5 obr. 5
Proudění kapaliny v hexagonálních buňkách směřuje obvykle ve středu buňky nahoru a podél okrajů buňky dolů. Jedná se prakticky
o kombinaci Rayleighovy-Bénardovy konvekce a nehomogenity povrchového napětí, která vzniká v důsledku fluktuací teploty v povrchové vrstvě tekutiny a tedy i fluktuací povrchového napětí. Teplotní gradient zde tedy neexistuje pouze v jedné dimenzi jako u Rayleighovy-Bénardovy konvekce, ale v rámci jednotlivých buněk ve všech třech dimenzích. Na myšleném průřezu Bénardovými buňkami bychom viděli Rayleigovy konvekční válce.
obr. 6 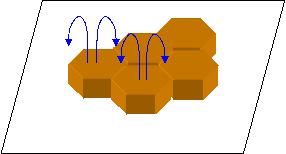  obr. 7 obr. 7
Mechanizmus vzniku Bénardových buněk si můžeme představit takto: p ředpokládejme, že v jistém bodě povrchu tekutiny nastane fluktuace 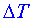 teploty od teploty v okolních bodech. Nechť např. teploty od teploty v okolních bodech. Nechť např. 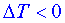 . Povrch má tendenci se smršťovat k tomuto chladnému bodu - k místu, kde je větší povrchové napětí. Kapalina zde tedy klesá dolů (místa na okrajích B. buněk). V jiných místech musí kapalina stoupat nahoru, přičemž se vzdaluje od chladného místa (středy B. buněk). Původní fluktuace . Povrch má tendenci se smršťovat k tomuto chladnému bodu - k místu, kde je větší povrchové napětí. Kapalina zde tedy klesá dolů (místa na okrajích B. buněk). V jiných místech musí kapalina stoupat nahoru, přičemž se vzdaluje od chladného místa (středy B. buněk). Původní fluktuace 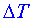 teploty způsobí konvektivní pohyb pouze tehdy, jestliže stoupající kapalina má dostatečně vysokou teplotu, aby udržela gradient povrchového napětí. To znamená, že teplotní rozdíl teploty způsobí konvektivní pohyb pouze tehdy, jestliže stoupající kapalina má dostatečně vysokou teplotu, aby udržela gradient povrchového napětí. To znamená, že teplotní rozdíl 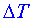 mezi dnem a povrchem kapaliny musí dosáhnout jisté kritické hodnoty. Faktory, které brání popsané konvekci jsou vedení tepla a viskózní jevy. mezi dnem a povrchem kapaliny musí dosáhnout jisté kritické hodnoty. Faktory, které brání popsané konvekci jsou vedení tepla a viskózní jevy.
Destabilizujícími mechanismy jsou tedy jednak přívod energie do systému, který lze vyjádřit členem 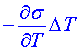 , (kde , (kde  je povrchové napětí), jednak ireverzibilní procesy, vyjádřené členy charakterizujícími viskozitu a teplotní vodivost. Bilanci sil nebo energií mezi oběma druhy procesů působícími protikladně lze vyjádřit pomocí bezrozměrného parametru, Marangoniova čísla (M): je povrchové napětí), jednak ireverzibilní procesy, vyjádřené členy charakterizujícími viskozitu a teplotní vodivost. Bilanci sil nebo energií mezi oběma druhy procesů působícími protikladně lze vyjádřit pomocí bezrozměrného parametru, Marangoniova čísla (M):
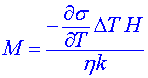 , ,
v němž H je hloubka vrstvy, 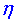 je dynamická viskozita, k je součinitel teplotní vodivosti. je dynamická viskozita, k je součinitel teplotní vodivosti.
Videonahrávka vzniku Benardových buněk: video (5MB).
Videonahrávka Bénardovy konvekce při nižším vertikálním teplotním gradientu: video (5,6MB).
Videa jsou zkomprimována v DivXPro(tm) 5.1.1 Codec, instalační program zde.
Zpracováno podle:
Coveney P., Highfield R.: Mezi chaosem a řádem, Mladá fronta, Praha 2003.
Duršpek J. : Moderní termodynamika v chemických a biologických procesech, Plzeň 2005.
Gleick J.: Chaos, Ando Publishing, Brno, 1996
Horák J., Krlín L.: Deterministický chaos, Academia, Praha 1996.
Krempaský J.: Synergetika, VSAV, Bratislava 1988.
Maršík F.: Termodynamika kontinua, Academia, Praha 1999.
Prigogine I., Stengers I.: Řád z chaosu, Mladá fronta, Praha 2001.
Štrunc M., Kheilová M.: Příklady vzniku disipativních struktur v nerovnovážných, nelineárních systémech, VUT Brno, 1998.
http://hmf.enseeiht.fr/travaux/CD0001/travaux/optmfn/hi/01pa/hyb72/index.htm
Obrázky: 1,4,5,6 autor, 2:(Horák J., 1996), 3:(Gleick J, 1996) 7:(Štrunc M.,1998)
|
|
|

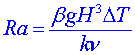 ,
,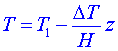
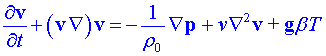
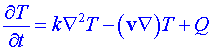
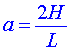 .
.
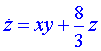 .
. 




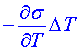 , (kde
, (kde 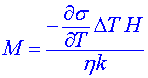 ,
,